Read the first 6 Pages: Chapt4Frst6Pages.pdf
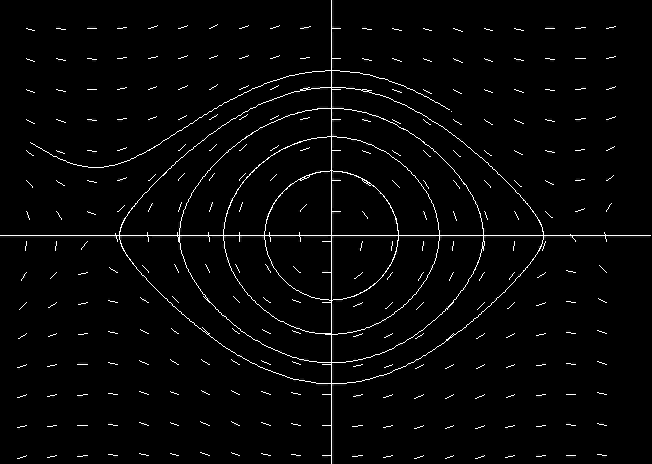
This movie shows a few orbits of a pendulum (i.e., solutions of the second order equation d^2 x/dt^2 = -sin(x) ) . Note that the solutions with small initial position and velocity are essentially circular, since they are very well approximated by the linearized system d^2 x/dt^2 = - x, i.e., the harmonic oscillator, but as we move away from the stable point at the origin, the orbits get progressively less circular and eventually we see an orbit where the pendulum swings “over the top” .
Here is a page of more detailed instructions for doing computer experiments involving the Pendulum and the Harmonic Oscillator and their relation. PendulumExperiment.pdf
Here is an animation of Keplerian motion that contains a graphical proof that Kepler's Law's of Motion (in particular the fact that orbits are ellipses and that the radius vector sweeps out equal areas in equal times—i.e., that angular momentum is conserved) implies that the potential energy of the central force must be inversely proportional to the distance from the center. For a full explanation, see: Kepler Orbits.pdf.