Click here to see the first 35 Pages
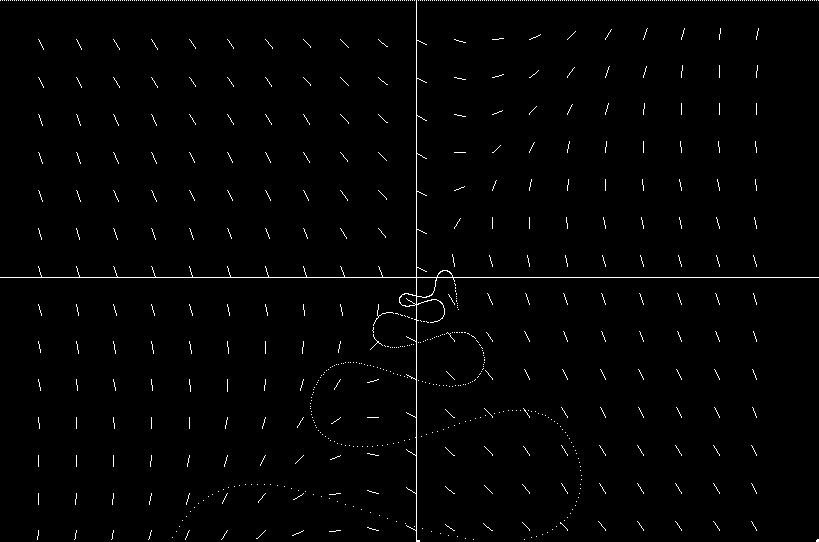
This movie shows the metaphorical “smoke particle blowing in the wind” mentioned on page 5 of the text. The path of the smoke particle is given by a dotted curve. The dots are laid down at a constant rate, so the distance between them gives an indication of the wind speed along the path. Notice how the wind keeps changing direction both in space and in time, and that the smoke particle keeps changing its direction to that of the local wind direction at that time.
NOTE: This movie was produced by a freely available mathematical visualization program called 3D-XplorMath. We encourage you to use this program to visualize differential equations. It is available in both Mac and cross-platform Java versions at 3d-xplormath.org.
Here is a whole family of one- , two-, and three-dimensional ODE applets produced using the Java version. (See: 3D-XplorMath ODE Gallery) We highly recommend these applets as a default playground for experimenting with all types of ODE.
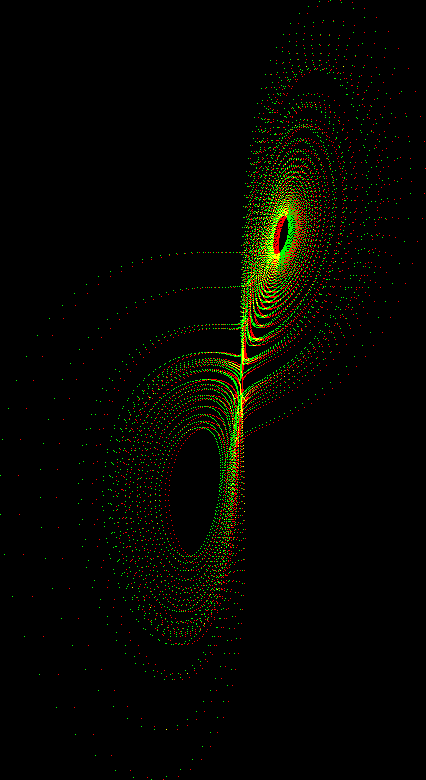
Lorenz_ode.mov; Lorenz_ode_stereo.mov (requires red/green glasses).
3D-XplorMath Java applet
This movie shows the evolution of a solution of the Lorenz ODE. This is the equation studied by Edward Lorenz that led him to make his famous remark about the flapping of a butterfly's wing in Brazil setting off a tornado in Texas.
The important thing to notice about these movies is the sudden jumps of the orbit between the upper and lower loops. Two orbits with very close initial conditions will stay close for a reasonably long time, but then one of them will make the jump considerably earlier than the other, and after that the solutions are far apart and un-correlated. This is the essence of chaotic behavior.
Here is a movie of another famous chaotic equation, the Rössler System. Here the point to notice is the way an orbit slows down greatly and then speeds up again as it moves around the phase space. Points that start out close together in the phase space will at first remain close together, but one will experience one of these speed changes well before the other and after that their paths will be far apart and uncorrelated.